Self-Similarity Code Book:

The enhancement method

Huai Li and his colleagues explored the use of fractal compression to enhance the microcalcifications in mammography (Li et al, 1995). The technique was to compress an original image using a hand constructed IFS and then generate the resulting image (a fixed point of the iteration of the IFS). This generated image was never the same as the original (fractal compression is lossy) so when one subtracts the two images one gets a representation of those areas of the image most un represented by the similarity transforms of the chosen IFS.

Figure 1 shows the results of a similar experiment that we conducted using the compression algorithm that came in a disk packaged in the book Fractal Imaging ( Ning Li, 1997, forward by Michael Barnsley).

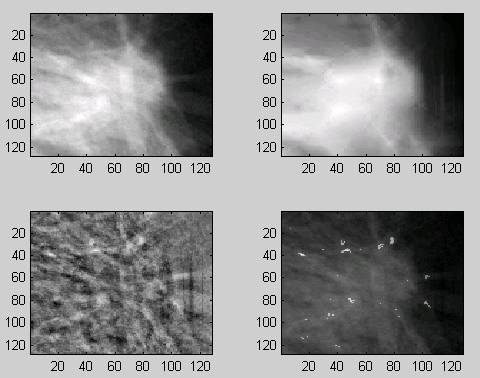
Figure 1: Experimental data on fractal enhancement of features

In running the experiment that produced Figure 1, we had no control over the selection of the IFS. The upper left corner image is the original normalized and cleaned windowed image from the GMAI image database. The upper right hand image is the fixed point of a IFS generated by the Iterated System’s commercial software (with a parameter set to encode only 80% of the resolution). The image in the lower left corner is the difference between the two upper images. This difference represents the part of the image having the greatest loss of original resolution. The lower right image is an enhancement of specific small areas where the local self-similarity is greatly different from the global self-similarity.

The objectives of both Fisher’s book (Fisher, 1995) and the Barnsley book (Nig Lu, 1997) is to reduce the loss in detail while increasing the speed of the compression. This is not our objective. Our objective is to identify kinds of self-similarity and associate classes of self-similarity to specific textures in images, and thus to specific processes that produce that texture in the image.

The process of pairing domains to ranges is a long process and can be accomplished in a number of ways. The process is nicely represented by Fisher’s Pseudo-code (page 19, Fisher 1995). The steps in this code are as follows:

1) Choose a tolerance level e.

2) Partition the full image into disjoint regions. Do this iteratively so that the first partition is composed of one element (the whole image) and the following partitions have more and more elements. This is often done by forming a quadtree partition where each level is related to the level above by inclusion and each level has four times the partition elements as the previous level. In the standard quadtree partition, each region is the same size.

3) At each iteration, of an image being partitioned into regions, a comparison is made between each element of the partition and each element of the partition at the lower level. The upper level provides a domain “pool” and the lower level provides a set of ranges. An enhanced domain pool is often formed by taking each of the partition elements, in the level above, and making eight copies using rotation by 90 degrees and flips. We want to find a contractive affine transformation that carries a reduced (averaged) domain to a range element and such at the root mean square is small. If the root mean square is small then the domain element is said to “cover” the range element.

4) If a range element is covered by a domain element, then an affine transform is easily solved for and written out.

5) If there is no domain in the domain pool that covers the range element, then the range element is partitioned in a new set of ranges and the domain pool redefined to search for a cover for one of more of these new ranges.

Ideally, the entire image would be covered by domains and the resulting affine transforms written out. This ideal is not often achieved, since there is a limit to the number of times one can partition an ever smaller set of pixels.

Variations in this process include the following:

1) the domain pool can be nominated to be other than just the set of elements in the partition “above” the partition containing the targeted range element.

2) The domain pool can be irregular in shape.

3) The pixels in a domain element are averaged into an array that has the exact size of the range element. If the reduction is one to four then one can average in four ways to get a averaged domain element. This reduction technique has many variations – some which may have specific arguments for using it. For example, the convolution of an indicator function (like a normal distribution) with a wavelet may pick up and enhance features of interest in the averaging step.

4) The enhanced domain pool may be formed by rotating at a degree other than 90. Taking the degree of rotation to be 10 would produce many more elements in an enhanced pool and perhaps capture better similarities.

5) Self similarity above the threshold might be recorded to allow a linking together of near similarity, or the development of some form of evolutionary programming to capture linkages between domain/range pairs and other domain/range pairs. This technique may lead us into a theory of the kinds of self-similarity that is seen in a single image, and also seen across a collection of images.