Index                      .

 

 

 

Full enumeration of SLIP primes

 

An advanced tutorial

 

Copyright (2002), OntologyStream Inc.

 

 

In the previous advanced tutorial, we find that 100% of the data in 1/100 of 14 mins of trunk data is completely described by three simple visual objects.   VisualAbstraction renders all of the data into categories, where each category is representing all of the elements that are exactly the same.  The pictorial icon is that set of categories with all of those relationships, and only those relationships, that are in the original data. 

 

We “see” the invariance in the data, and relationships between the invariance in the data and we see all of this invariance all at once. 

 

Invariance can be defined as being exact, or being exact after the application of a specific transformation.  For example, “here” and “ehre” is the same after a juxtaposition of the first two letters in one of the two words.  One can replace the notion of exactly the same with the notion of similar in this specific way.  No one has yet done this as a preprocessor to the SLIP analysis. 

 

Before one can have the right to do this type of advanced work, there must be a better social understanding of the nature of abstraction, language and knowledge.  For example, visualAbstraction is of the same substance as mental abstraction.   People who need to understand theses nature should reflect, for a moment, about the positive counting numbers. 

 

The positive counting numbers are distinguished from zero and the negative counting numbers and of course from real numbers, complex numbers and tensors.  The real numbers, complex numbers and tensors are derived from counting and notions of nearness and orderliness.

 

But, as in the tri-level notion from stratified theory, there are variations in the substance of mental abstractions.  The positive integers, for example, have an exact correspondence with things that occur in the natural world.  But do negative numbers have an exact correspondence with something that occurs in the natural world?  We have things that are three in number.  But do we ever we have something that is minus three in number?

 

Does one ever have something that is the length of an irrational number?  Well, the answer here is yes.  This exact correspondence to the things in the natural world is fleeting.  And so we find that the relationship between those mental abstractions, which are about numeration, does not produce an absolutely consistent coherent framework.  We are lead into Russell’s paradox, and eventually to the work of Godel, Cantor and Zenkin. 

 

One should expect that work on visualAbstractions have similar difficulties. 

 

But the compression of data into categories is useful.  We are beginning to show that these categories “are” the data, in the sense of “standing in for” the data.  Again, as an example, one can see all of the data in this 1/100 of the 14 mins of Internet traffic in three visual abstractions. 

 

One can retrieve and route data using these three visualAbstractions since one knows from the details of each of these visual objects all detail that exists in the data.

 

VisualAbstraction is an exceeding simply notion.  A specific conjecture sets up a view of the original data and this view produces a specific theory of relationship.  Only those categories of invariance in the data that support this theory of relationship are brought into a derived data set.  The precision and recall is perfect.

 

One sees that already the conjecture filters the original data set.  In theory, the conjecture can be any statement in logic where the logical primitives are the names of columns of data.   This logic plays the role of a query language. 

 

The query is part of a large process of investigation and analysis.  The conjecture produces this derived data set.  Once the derived set is produced, this derived set is subject to 100% compression into a theory of category type.  This theory of category type is expressed in the visual icons that we are seeing. 

 

Before we move into the tutorial proper, one should reflect on the reality of any of the standard data compression algorithms.  The compression dictionary is core to any of these, even if the use of a dictionary in the bit stream compression is sometimes implicit rather than explicit.  So even without a tab delineated input to eventChemistry, the compression dictionary of any of these schemes will produce a collection of SLIP-type atoms. We need only to produce event records in order to have the datawh.txt file. 

 

In our study of fables we wrote a natural language parser that looks for a correlation between the occurrence of a noun and the occurrence of a verb in sentences.  This becomes a generalization of Latent Semantic Indexing when we look to the correlation between the occurrence of a word and the text unit that the words occur in.  The diagonization of a matrix in the standard LSI simply confuses what is a straightforward production of a abstraction.  The same abstraction is easily produced by the specific analytic conjecture that we use in the fable study.  The diagonization of a matrix forces a global resolution of the relationships that are initially only known as a pair wise evaluation function:

 

Is this word token in this text unit?

 

In both LSI and vA, the functional load of the word token in the collection of all text units is given.  In vA, but not in LSI, this functional load is then viewable in the event chemistry.

 

Section 1  

 

The comments in the introduction suggests one can take random samples (splits) to identify and bring into high resolution the various “characteristic objects” in event spaces.  These objects will be viewable in a new browser that Cedar Tree Software has under development.

 

 

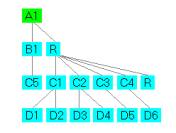
Figure 1:  A SLIP framework showing seven major primes and a residue

 

We start this tutorial with the 2,354 K zip file called simpleComplex.zip.  Download the zip file and unzip into an empty folder.   We will see four browsers and the Data folder.

 

 

Figure 2: The simpleComplex project

 

The browsers have been changed slightly and renamed.  One should open the SLIPWH to see the analytic conjecture being used.  SLIPEvents is best called through mouse clicks in SLIPCore (formerly call SLIP Technology Browser).

 

Opening the SLIPCore will take about 20 second.  During this period, the Core will complete four steps, including the following:

 

 

An I-RIB structure is established in memory and a referential information base is composed using tensor structures, ordered lines and sets.  An index is established to allow a report to be generated.  This report is the set of all records from datawh.txt that was involved in the definition of one of the nodes of the SLIP framework.

 

Once the report key is set, then the Core is able to load from the Data Folder, if the data in the folder has been developed at some previous time using the import and extract commands.  If these commands have been issues at this data folder, then the folder will have an A1 folder inside the Data folder, and perhaps some subfolders.

 

If one has an A1 folder already, then one commands, “load” to see the SLIP Framework.  In this data folder we have already pre-developed the SLIP Framework and commanding load will show Figure 1. 

 

The SLIP Framework in Figure 1 is significant in that the ending nodes of the Framework is a unique prime decomposition of the full 14 minutes of Internet Truck data provided to OSI by AboveSecurity Inc. 

 

If one wishes, one can make a copy of the entire folder simpleComplex and delete all files inside the Data folder except the single file datawh.txt.  One can check to see that this file contains 6,413 K of tab delineated ASCII text.

 

 

Figure 3: A copy of simpleComplex

 

Let us review how to develop the analytic conjecture and the A1 node.  Open the WH browser and command a = 3 and b = 4.  Then issue the command pull and export.  The pull command will take about 8 seconds and the export will take about one minute.   One can watch the response messages to see how the KOS interpreter is developing the data on invariance.  The final part of the export is to produce a sorted file for Pairs, atoms and links.  These files are placed into the Data folder for re-use later. 

 

Closing and opening the WH later on will not show the information in the Warehouse Properties window unless the pull and export commands are reissued.  This bookkeeping is part of the machinery that we have left undone, since we envision the development of integrated enterprise solutions for various markets.  This bookkeeping is just one of those things that one has to work around until there is a specific vertical enterprise solution developed. 

 

Before closing the WH we copy down the following facts:

 

 

A note on the production of pairs. 

 

(a1,b) (a2,b) à  < a1, b, a2 >

 

The formalism < a1, b, a2 > is called a syntagmatic unit and is the basic element of any ontology.  This is often two concepts and a relationship, but the interpretation of a syntagmatic unit can be more general that this.  The production of 625,667 syntagmatic units from only 120,246 records is due to a combinatorial process that is perhaps only understood clearly if not has thought a lot about set theory and number theory.  But the issue can be explained easily given about 20 minutes and a blackboard. 

 

From the 625,667 syntagmatic units we find only 1,886 types of b values.  In this case the b vales are destination ports.  By guess, I imagine that there are perhaps 3000 destination ports referenced in the 14 minutes of data.  But only 1,886 of them are involved in the relationship we have “data-mining” for.  Using a different analytic conjecture will get a different set of atoms, links and syntagmatic units. 

 

There is an important philosophical issue to address here, and eventually this issue must be addressed by peer-reviewed research.  The 14 minutes of data has structure because the events that occurred in these 14 minutes have structure.  So perhaps almost any reasonable analytic conjecture will “measure” the event types that are occurring “in the data”.  If someone understands which analytic conjectures are being used to measure the bit stream, then one will be able to develop a means to disguise events so that the specific conjecture used will not see the event.  One reason why OSI is insisting on a National CDKB is so that the light that shines with SLIP can be seen and used to identify those bad type events that are occurring and prepare for the next Cyber War. 

 

Returning to the tutorial, we will find the number of atoms by using the SLIPCore browser.  Use the Core browser in copy of simpleComplex to develop the atoms.  As before, the start up process ends with “Report key Column set to 3” message being issued by the KOS interpreter to the response message line.  One has to now command import and extract. Import takes the files produced in the WH and re-maps them to memory. 

 

It is possible to have some problems here as we have not finished optimizing the objects that Microsoft uses to produce a memory map.  Call us if you have some difficulty. 

 

After the import and extract processes are complete, one can click once on the A1 node to produce the 1,456 atoms that are in this data set. 

 

So close all of the browsers and return to the simpleComplex folder and open the SLIPCore browser.  Command the browser to load.  

 

 

Figure 4: the A1 node’s limiting distribution

 

The distribution of atoms in Figure 4 is produced by clustering the 1,456 atoms using over 6,000,000 iterations of a question about whether an ASCII string of length between 10 and 30 (the possible member) is in a large set of ACSII strings of length 10 – 30.

 

The number of potential members is actually quite large.  This number is 1,456*1,456 or 2,119,936.   The size the set being asked about is 625,667.   We need to ask and receive a correct answer to this set membership question 6,000,000 times.  So the computational problem simply seems impossible to do on a desktop computer. 

 

How is this done?  Well let us not answer this question here, but rather simple see that it is done in about 14 minutes.

 

Having clicked on A1 once (it is really important to not double click on A1) issue the command random to produce a random scatter to the circle.  Now find a timer to look at and when the second hand is at 0, command c 6000 or cluster 6000.    You will see the clustering process develop until this difficult set membership question is asked and answered 6,000,000 times.  Outside of the single large spike you will see the changes being made to the distribution locally have stopped because the stochastic process has reached its omega cell – the term for a stable limiting distribution. 

 

The fact is that without the theory that we developed, the process of clustering takes about 5 hours using an optimized FoxPro Rushmore index. The theory and algorithm has been made public domain, and can be reviewed. 

 

Once the iterations have stopped, then we need to review the process.  The B1 node contains 1219 atoms that we bracketed and moved into the B1 category from A1 by using the bracket command:

 

145, 155 -> B1

 

when the A1 node is selected (and the old distribution existed.)   The command residue takes everything not already moved to the second level and places these atoms into the R category. 

 

Section 2: On the number of objects we are addressing

 

In addition to the six primes { D1, D2, D3, D4, D5, D6 } we have 116 compounds in the C-level residue and 53 compounds in the central event { C5 }.  The central event is almost a single prime; however, I need to do again the experiment and cluster to 10,000,000 to settle out all of the movement in the distribution. 

 

Click once on the R node (at the second level in the framework) to see that there are 236 elements in this residue.  Categories { C1, C2, C3, C4 } are simply the atoms regions where I saw large primes.  Inside of these categories we find large number of small primes and six large (having > 3 atoms) primes.  The residue in the C level also has a large number of small primes.

 

You can change the stationarity of the limiting distribution in the C-level residue by clustering a few million times.  Almost nothing will change. 

 

So this implies that in the residue we have

 

 

Remember that simple compounds have only one relationship.

 

 

The large cluster that we have put into category C5 is a prime with 1887 atoms that has 53 simple compounds that are organized into one complex compound

 

The ability to get into and visualize what are the visual forms of the atoms and links is done in a number of ways.  At OSI we still need perhaps 4 – 5 weeks of development time to sort of the visualization of the complex compounds in a three-dimensional format.

 

 

Appendix The table of all primes

 

In addition to the six primes { D1, D2, D3, D4, D5, D6 } we have 116 compounds in the C-level residue and 53 compounds in the central event { C5 }.

 

Table 1: The 116 simple compounds in the C-level residue

 

1497        65515

43834      65515

2497        57868

4491        53876

4841        52098

2627        47129

2741        46222

2842        46340      44551

4647        44548

2130        35669

7227        58071      39636      36305      35645

256          6459        59738      45057

1342        33159

3453        32683

12147      29554      8231

12590      8232        29485

12846      29485

65535      65024      56064      47359      28915

2872        56064

14895      29808

25639      29808      28276

29498      29808

25966      30311      27709

27749      28784      26988

25955      8290        2675

26979      8310        26734      28526

20322      26368

4911        26368

25705      26656      26144

12134      28261      26990

29231      28261

29796      28261

30582      28261

8253        28261

11878      26990

12137      26990

12139      26990

12142      26990

25972      26990

26400      26990

28015      30066

29556      25705

29440      28260      25459

8306        28260

30067      8306        8293        25441

30057      8293

11882      26479      25396

2675        29811

11875      28276      24950

25701      28015

30066      28015      24948

25448      24948

28530      24948

25971      28515      24930      29556

25455      27694

25459      27694

1533        24091

6971        64948      23457

2579        21764

4132        21067

4727        19916

768          2110

27756      27497      19305

15105      54812

12097      27763      17747

25866      27763

27745      25465      16979

25461      29541

26459      29541

29216      29541      16752

1024        38941      16547

29742      26995

29793      26995

29797      26995      16494

12337      14138      13626

13875      13620      13612

14896      13621      13369

12342      29279      13365

11296      13623      13363      13351

8224        24953      13344

8310        13367      13110

12838      26173      13104

12334      14648      12848      8231

13614      12848

11786      28526      12583

27936      29801

30313      29801      12832      12576

20557      21743      12576

12851      12576

29732      12427

12339      14647      12602      12346

1539        12323      12322

25193      29231      12147

29045      12147

30051      12147

28001      28521      26469      24435

29487      26469

26473      27759      11875

28525      11875

28533      11865

12130      8231

12327      8231        11833

28271      8231

29295      8231

15872      25972

16752      25972

14641      14388      11321

29812      8808

5632        58371      50946      23298      19715      16899      11011

22            1008

2637        10030

24942      29556      10016

29279      29556

28777      26144      10016

25189      10016

30569      10016

 

Table 2: The 53 compounds of the Category C5

 

30057      29553

12134      25971

12142      25971

12148      25971

29472      25971

8290        25971

11875      25965

18025      25448

25970      25448

6400        21002      41738      36106      24074

57603      17933      2066

28001      12137

26990      12130

1205        6667

1966        6667

9727        59408

33723      50180

35148      49424

21714      44037

60393      31504

35652      30468

36327      29711

42601      2565

768          19468

20260      15123

41517      12554

16752      11786

19809      11786

2304        4608

3072        4608

256          33939

13607      27756

24940      27756

136          1

27752      1

1              0

104          0

139          0

15360      0

20224      0

23425      0

26712      0

26740      0

27233      0

27904      0

31977      0

33768      0

776          0

87            0

91            0.  

 

 

0              9732        9217        8452        8195        8192        7939        7428        65280      65025      64256      64004      63755      63492      62980                62724      62541      60676      59400      57982      57617      56842      55535      52384      51992      51730      5124        5120        50562                50306      49473      49421      49409      49163      49153      46270      4608        4530        43010      42502      41898      4100        39936      3988                38929      38667      3596        35840      35590      35076      34128      33939      33807      33540      3342        3330        32768      32517      3073                30376      2840        27756      27659      2564        24329      23812      23808      22532      22283      22027      21003      21000      2053        2048                19972      19408      19224      18688      18683      18176      1797        1796        17860      17744      1774        17156      16388      1542                15108      15105      12556      11781      11780      11021      1043        10244      1              0

 

 

13568      9732        9220        8964        8452        773          7428        7172        6660        65028      64772      64516      64260      64004      63492                63236      62980      62468      61956      61700      6148        60932      60676      58628      57348      57092      56580      5636        54788                52996      5124        49668      4868        47876      4612        45060      4356        4100        3844        38404      33796      29188      2820                26116      261          25860      2564        22276      2053        2052        20484      20228      19972      18180      1797        1796        17668                16900      16644      15620      15364      14852      14084      13060      12804      12036      11780      10756      10244      0

 

20480      9989        9988        9747        9745        9744        9743        9741        9737        9491        9489        9477        9233        9232        9229        9225                9222        8977        8976        8969        8968        8721        8720        8715        8708        8467        8465        8461        8210        8209        8208                8207        8202        8200        7955        7953        7940        7699        7697        7692        7691        7690        7441        7435        7430        7187                7185        7184        7179        7173        6929        6923        6675        6673        6667        65298      65297      65296      65294      65293                65291      65289      65285      65041      65039      65038      65032      65031      64785      64777      64529      64528      64272      6419        6417                6416        6413        6411        6409        6406        6405        6404        64017      64016      64014      64010      63761      63760      63756                63754      63753      63752      63749      63748      63505      63504      63502      63499      63498      63493      63249      63248      63246                63242      63240      62993      62992      62988      62737      62736      62732      62729      62728      62725      62481      62480      62478                62472      62225      62224      62213      61969      61968      61967      61962      61957      61713      61706      6163        6155        6149                61457      61456      61455      61454      61452      61450      61449      61448      61445      61444      61201      61199      61198      61197                61194      61190      61189      60945      60944      60943      60940      60938      60937      60933      60689      60681      60677      60433                60432      60431      60421      60420      60177      60173      60164      59921      59920      59914      59910      59666      59665      59664                59663      59659      59656      59655      59652      59409      59408      59406      59405      59397      59396      59154      59153      59152                59146      59145      59144      59141      5906        5905        5899        5893        58897      58896      58895      58888      58885      58641                58638      58637      58386      58385      58384      58382      58373      58372      58129      58128      58126      58121      58116      57874                57618      57614      57611      57609      57604      57362      57361      57360      57350      57349      57106      57105      57095      56849                56844      56841      56593      56592      56586      56581      5651        5647        5646        5643        5640        5637        56338      56337                56332      56330      56325      56081      56080      56078      56076      56074      56068      55826      55825      55824      55818      55817                55570      55569      55566      55565      55314      55313      55312      55309      55308      55306      55300      55058      55057      55051                55050      55049      55044      54802      54801      54800      54799      54794      54792      54790      54544      54537      54533      54532                54288      54282      54277      54276      54034      54032      54026      54020      5393        5390        5386        5381        53778      53776                53775      53769      53765      53522      53521      53516      53514      53512      53509      53266      53265      53260      53259      53253                53009      53005      52754      52753      52752      52750      52746      52741      52497      52496      52487      52485      52484      52241                52240      52239      52236      52234      52230      52228      522          51986      51985      51978      51977      51972      51729      51728                51722      51721      51716      51474      51473      51472      51466      5134        5131        5126        51218      51217      51215      51212                50962      50961      50957      50949      50706      50704      50702      50698      50449      50446      50444      50194      50192      50191                50189      50180      49938      49936      49935      49934      49933      49924      49677      49671      49424      49422      49413      49170                49169      49168      48913      48909      48906      48900      4883        4881        4879        4878        4875        4873        4870        4869                48658      48657      48654      48653      48402      48397      48395      48394      48388      48146      48138      47890      47889      47887                47883      47882      47880      47877      47631      47621      47620      47372      47370      47118      47114      47109      47108      46865                46852      46607      46603      46602      46598      46353      46351      46346      46344      46341      4623        4619        4618        46097                46096      46095      46091      46090      46088      46085      45840      45839      45837      45834      45828      45584      45583      45581                45572      45327      45323      45322      45316      45073      45071      45070      45066      45065      44818      44815      44813      44810                44804      44559      44554      44549      44304      44303      44302      44301      44293      44292      44048      44047      44037      43794                43793      43792      43791      43785      43780      4369        4368        4363        4359        43536      43530      43524      43282      43280                43278      43273      43269      43268      43022      43018      43016      43013      42766      42765      42762      42758      42757      42756                42512      42509      42505      42501      42257      42255      42254      42246      42245      41999      41989      41745      41743      41742                41740      41738      41732      41486      41485      41482      41233      41230      41220      4115        40975      40965      40721      40717                40715      40709      40466      40461      40453      40210      40209      40204      40202      39951      39949      39946      39697      39685                39442      39432      39430      39429      39428      39186      39185      39182      39176      38930      38927      38926      38924      38920                38917      38916      38674      38673      38671      38666      38664      38661      3859        3858        3857        3853        3851        3850        3845                38415      38410      38161      38149      37906      37904      37903      37648      37647      37644      37642      37394      37391      37389                37388      37382      37381      37380      37135      37132      36882      36880      36879      36876      36875      36874      36870      36625                36623      36621      36619      36613      36612      36369      36367      36365      36356      36106      36100      3599        3595        3594        3593                3589        35855      35853      35852      35844      35599      35341      35340      35332      35087      35083      34833      34828      34826                34821      34577      34572      34321      34319      34317      34316      34313      34060      34057      34053      33798      33554      33551                33547      33546      3344        3340        3339        3337        3333        33297      33290      33043      33041      33039      33034      33028                32786      32785      32528      32527      32524      32273      32272      32270      32269      32266      32019      32015      32012      32011                32006      31761      31753      31748      31504      31502      31492      31251      31249      31247      31245      31237      30995      30994      3091                3082        3081        3077        30739      30737      30483      30481      30472      30469      30468      30226      30225      30223      30216                30215      30213      30212      29970      29965      29957      29956      29713      29711      29708      29702      29458      29455      29454                29452      29450      29445      29203      29202      29201      29199      29196      28944      28943      28941      28940      28934      28932                28691      28688      28685      28678      28677      28433      28432      28431      28428      28426      28424      28420      2832        2827        2826                2821        28178      28172      28169      28164      27923      27915      27914      27658      27411      27403      27402      27397      27149                27147      27146      27145      27142      27140      26895      26894      26890      26888      26885      26638      26634      26629      266                26383      26378      26373      26128      25871      25866      2579        2576        2573        2570        2567        2565        25618      25616                25615      25610      25605      25604      25361      25355      25354      25353      25103      25100      25099      25098      25097      25092                24851      24849      24847      24842      24838      24837      24595      24591      24587      24586      24336      24081      24080      24079                24074      24073      24071      24068      23827      23826      23824      23823      23819      23571      23569      23567      23566      23565                23563      23562      23557      23315      23307      23303      2322        2320        2312        2309        23059      23057      23056      23051                23047      23045      23044      22801      22800      22799      22547      22545      22544      22543      22539      22289      22288      22285                22280      22277      22035      22033      22028      22026      22024      22022      22020      21778      21776      21773      21771      21521                21520      21512      21259      21254      21253      21009      21006      21004      2067        2066        2060        2059        20495      20493                20492      20487      19986      19731      19729      19726      19717      19471      19470      19468      19467      19461      19219      19218                19216      19215      19211      19205      18963      18962      18957      18950      18949      18948      18707      18701      18699      18696                18694      18450      18445      18437      18194      18191      18189      18184      1811        1810        1808        1803        1800        1798                17936      17935      17930      17681      17679      17676      17423      17421      17171      17167      17162      17157      16915      16911                16909      16659      16658      16655      16651      16645      16402      16400      16393      16147      16145      16144      16139      15890                15889      15887      15886      15885      15879      15876      15633      15629      15626      1555        1554        1551        1550        1549                15379      15377      15372      15365      15123      15121      15113      15112      15109      14865      14861      14860      14611      14609                14608      14355      14353      14346      14345      14341      14340      14097      14095      14089      14087      14085      13843      13841                13839      13831      13829      13828      13587      13574      13329      13322      13317      13075      13073      13071      13069      13061      1298                1296        1291        12819      12817      12816      12805      12561      12560      12557      12554      12549      12299      12293      12048                11795      11792      11786      11784      11782      11538      11537      11280      11276      11275      11273      11027      10771      10768                10766      10508      10506      10505      1042        1041        1038        1030        1029        10257      10256      10253      10250      10248                10247      10245      10001      773          64004      63755      63236      62980      62724      62468      61956      61700      6148        60676                59400      58628      57617      56580      54788      52996      51730      5124        49668      49421      38929      35590      35076      33807                33796      33540      29188      27659      26116      261          22532      22027      21000      20484      18180      16900      16644      1542                15108      11021      10756      10244